Esta es la dinámica de cómo una esfera de materiales plásticos con un dimámetro aproximado de ~5.95mm, viaja a través de un cañón de entre 6.01mm a 6.23mm, acelerada por la diferencia de presión ambiental. Es de creencia común que la bola inicia su singladura desde el principio del cañón por la cámara del hop up. Estoy aquí para desenmascarar este mito.
Apartado 1: Los principios básicos del airsoft
Presión atmosférica en el final abierto del cañón, contra aire comprimido en el otro extremo. La diferencia de presión a través de la bola la cual se encuentra en la frontera de la alta presión del cañón, es el vehículo que la acelera a través del mismo. Es importante tener en cuenta que la diferencia de presión en la bola, se reduce en su trayectoria por el tubo del cañón, porque, a la par que la bola se mueve, el volumen de aire detrás de la bola se incrementa. Puesto que se establece el volumen de aire comprimido, la presión debe disminuir en consecuencia. Esta aceleración empieza alta y se reduce.
Hop up: el hop up es un dispositivo usado para corregir la trayectoria parabólica del proyectil a algo más plano. Esto extiende/incrementa el alcance de un arma lúdico deportiva de airsoft. Las armas convencionales de proyectiles no usan este sistema, ya que tienen velocidades de proyectil mucho más altas, con lo que la caida se hace menos notoria. El hop up sólo es posible en el airsoft, porque el proyectil es esférico. La aplicación de un retroceso nos permite usar el Efecto Magnus para aplicar una fuerza vertical aerodinámica al proyectil para oponerse a la gravedad.
El Efecto Magnus: el Efecto Magnus es cuando una esfera giratoria o un cilindro tiene aire en movimiento sobre él, trnasversalmente a su eje de rotación. Un lado se opone al flujo de aire y lo ralentiza por su fricción y causa una región o zona con una presión más alta. El otro lado está girando en la misma dirección que el aire, y no tiene ningún efecto, o lo acelera por la fricción de la superficie de la esfera/cilindro, reduciendo la presión del aire, lo que crea un are/zona de baja presión. Esto crea una diferencia de presión a través de la esfera/cilindro, que a su vez, imparte una fuerza sobre él.
El Principio de Bernoulli: el Principio de Principle establece que un fluido en estado de trabajo se mueve más rápido, y los fluidos rápidos tienen menos presión. Las desviaciones extienden el fluido, lo ralentizan y causan baja presión. Esto es importante para comprender los efectos del aire que pasa alrededor de la bola dentro del cañón.
El Efecto Coanda: el Efecto Coanda es la tendencia para un fluido el ser atraido por superficies circundantes o cercanas, y por extensión, seguir a una superficie curva. Esto es importante porque las bolas son curvas. Así que el Efecto Coanda prevalece en esta aplicación.
Apartado 2: El mito - la bola pasa por el cañón una vez que ha rozado la goma del hop up, la goma contra la leva del hop up
Me temo que no, mis desinformados amigos, y veamos cuatro simples razones del porqué:
- En primer lugar, si la bola está produciendo roce en la parte superior del cañón, significa que no hay aire entre el espacio de la parte superior de la bola y la pared del cañón, con lo que no se produce Efecto Magnus, y no se produce fuerza vertical que la mantenga contra la parte superior del cañón. En el mejor de los casos, la bola se encontrará rebotando contra la parte superior del cañón.
- En segundo lugar, no hay casi aire (en comparación con lo que sería volar al aire libre) pasando alrededor de la bola. La presión en la parte delantera es practicamente atmosférica, con lo que la presión en la parte trasera es significativamente más alta que la atmosférica, y esa diferencia de presión acelera la bola, que relativamente es de baja masa, y con movimiento no restringido, con lo que la aceleración es muy rápida. La cantidad de flujo de aire es muy pequeña, con lo cual, experimenta (la bola) una pequeña fuerza vertical debido el Efecto Magnus.
- En tercer lugar, el Principio de Bernoulli establecen que un fluido de trabajo se mueve más rápido, y los fluidos más rápidos tienen una presión menor. Las desviaciones separan el fluido, lo ralentizan y causan baja presión. Si la bola se desvía de su centro, entonces el Efecto Bernoulli la centrará de nuevo. Esto también significa que cualquier flujo que baje la presión lo hará delante de la bola.
- En cuarto lugar, finalmente y quizás, lo más importante, imaginemos por un momento que una bola es irrealmente pesada, o por alguna razón se queda fijada en su sitio dentro del cañón, pero todavía con un efecto de contragiro masivo. Tiene presión atmosférica de aire en su parte delantera, y aire de alta presión detrás de ella, y las fuerzas del aire están más allá de la bola estacionaria. Con relación a la corriente de aire que se mueve sobre la bola, tiene ahora un efecto de giro hacia delante, y no hacia detrás (contragiro). Entonces cualquier efecto Magnus que se experimente mientras está dentro del cañón, será hacia abajo en lugar de hacia arriba.
Apartado 3: Respaldo
Y siendo éste el caso, hay dos maneras de comprobar si tengo razón:
- Construir un banco de pruebas con una cámara de alta velocidad y un cañón transparente para grabar en video la bola en su recorrido por el cañón y observar la realidad de la situación.
- Hacer un estudio Dinámica de Fluidos por Ordenador (DFO) para crear el modelo.
La opción del paso 1, me tomaría demasiado tiempo, esfuerzo y dinero. Quizás pudiera usar un cañón de plástico, y que me prestaran una cámara de alta velocidad. Observar el límite del cañón y el aire, podría ser difícil. Podría solucionarse usando humo, o quizás otro gas coloreado para impulsar la bola. Desgraciadamente todos los gases coloreados que conozco son tóxicos. Podría usar humo, producido por una máquina de humo, o tal vez vapor de agua. Todas estas soluciones tienen el mimso problema: no son aire, con lo que sus dinámicas serán diferentes debido básicamente a las variaciones en densidad, viscosidad, y un sinfin de otras cuestiones. El cañón y la bola probablemente también necesiten ser marcados para obtener cualquier tipo de información útil del experimento. Como hacer, podría llevarse a cabo, pero con un montón de trabajo de por medio, y realizar la filmación.
Esto nos deja con el punto 2, la DFO. Se trata de un método por el cual, un ordenador hace los cálculos de un modelo físico matemático, usando principios de base. Es esencialmente más económico que el primer método, si tienes un ordenador con ciertas capacidadesy el sofware adecuado. Tomará un poco de tiempo el generar la geometría tridimensional y configurar el modelo, con lo que lo haremos por DFO.
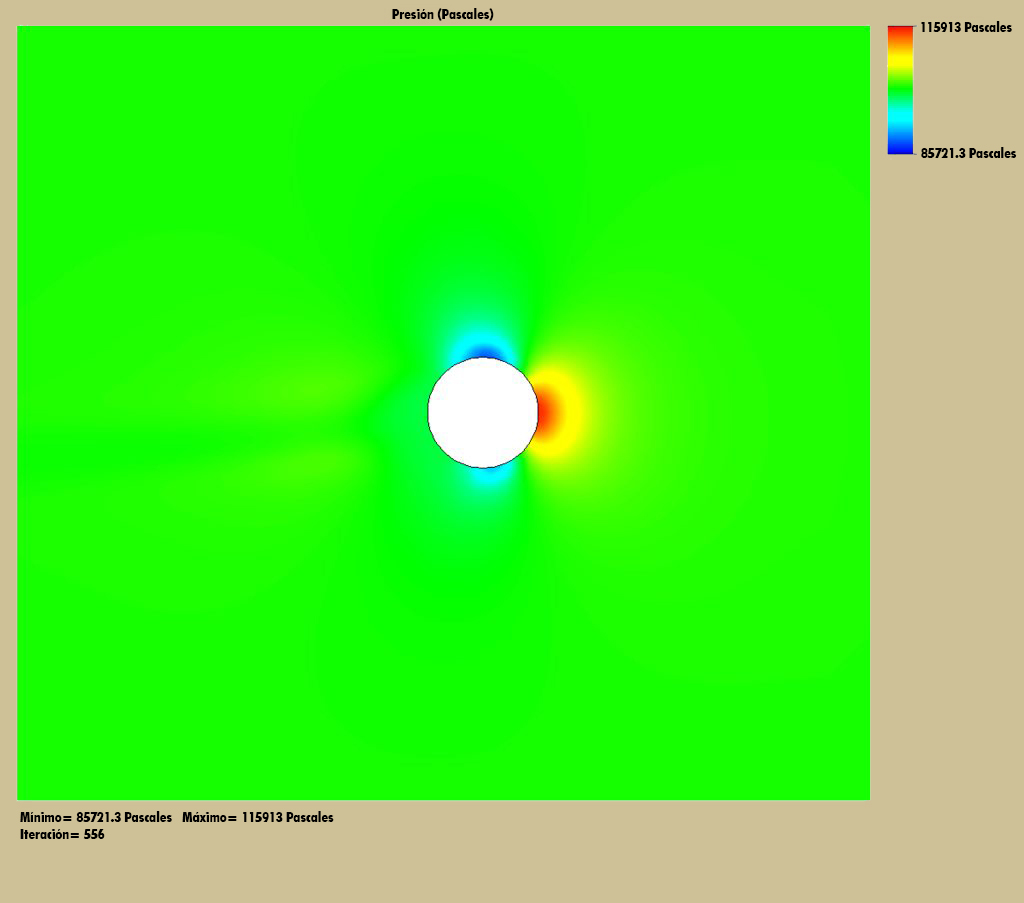

He asumido y aplicado una superficie con una rugosidad de 0.4um para una bola de plástico pulido y para identificar el cañón. Si tienes valores medidos y conocidos para cualquiera de las superficies mencionadas antes, podrías pasármelas para mejorar el modelo.
Y es el eje vertical, Z es el eje del cañón y X es el eje lateral.
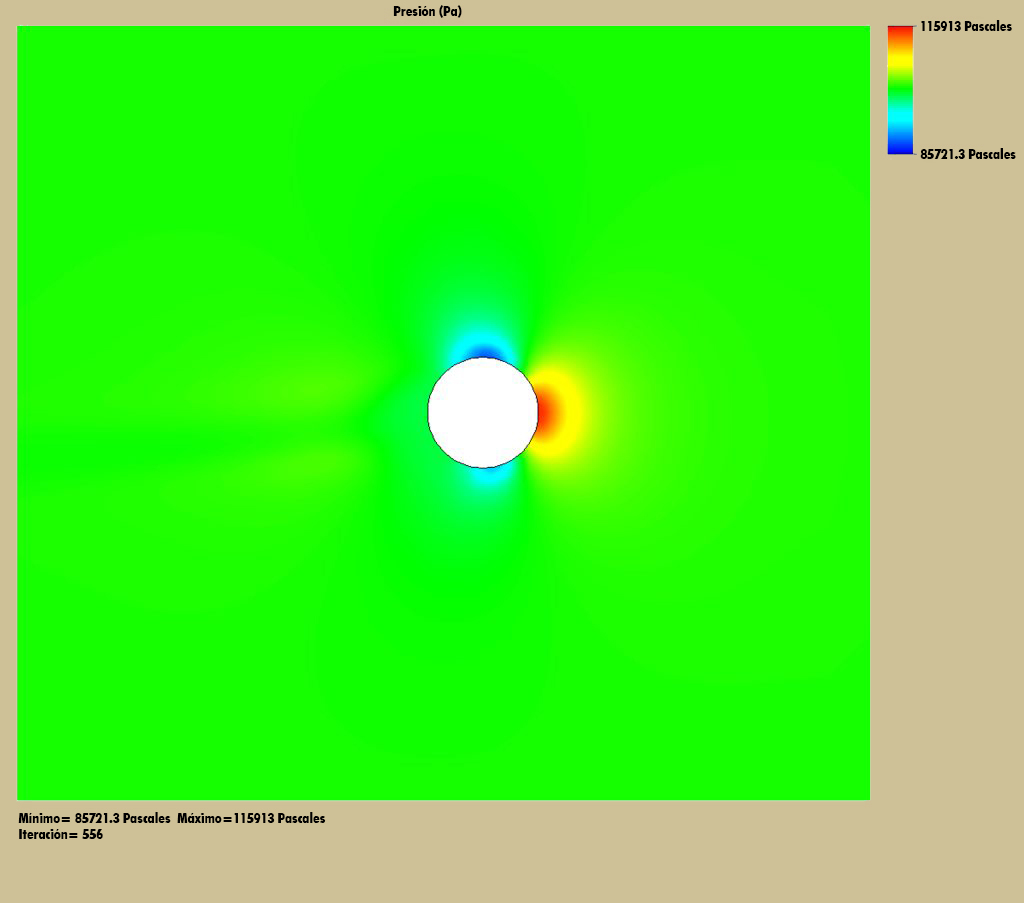
En primer lugar, he tenido la oportunidad de que el programa modela el efecto Magnus de manera correcta. Para hacerlo, modelé una bola en flujo libre de aire. La bola presenta efecto de contragiro sobre el eje X de 115,000 rpm, y el aire se mueve a su alrededor a 106.68m/s.
Fuerza (X) [N] -0.000143715
Fuerza (Y) [N] 0.074027023
Fuerza (Z) [N] 0.07616237
Esto muestra que hay un movimiento lateral mínimo, y en éste caso, la fricción de la bola es aproximadamente igual a la elevación del efecto Magnus.


Fuerza (X) [N] -0.000197728
Fuerza (Y) [N] -0.007692067
Fuerza (Z) [N] 20.24816055
Aquí pudes ver que la fuerza lateral es más o menos la misma, ya que hay una gran aceleración, como era de esperar, y que la componente vertical es un orden de magnitud menor y negativa. Esto significa que el Efecto Magnus se invierte, y una décima parte es tan fuerte como el flujo libre.
Estos resultados son como me esperaba. Es importante resaltar que el software que estoy usando no puede modelar movimiento inducido. Como tal, es un modelo de estado estacionario. Es decir, la cantidad de aire que pasa sobre la bola es mucho mayor que en la realidad porque está artificialmente fija en el modelo de ordenador. En la realidad, el Efecto Magnus y la Fuerza Lateral serían mucho mejor. Por mencionar un dato de interés para algunos de vosotros, la tasa de flujo de masa en la boca del cañón a presión atmosférica fue de 0.001219999 kilogramos por segundo, es decir, nada. Ya que la bola de éste modelo no se mueve, todo ese aire sale por la bocacha del cañón despues de sobrevolar la bola.
Con esto queda demostrado que el Efecto Magnus, mueve la bola del centro del cañón, pero hacia arriba, más que hacia abajo.
Es importante tener en cuenta que cualquier variación desde el centro exacto del cañón, se contrarresta con el Principio de Bernoulli y el Efecto Coanda, para devolver la bola al centro. Para probar esto, modelé la bola fuera del centro del cañón, como si el Efecto Magnus la hubiera movido hacia abajo. Estos son los resultados:
Fuerza (X) [N] 0.00212832
Fuerza (Y) N] 0.142694822
Fuerza (Z) [N] 20.27990608
La fuerza lateral es ahora viente veces más grande, y sospecho que esto se debe al desprendimiento de flujo en el otro lado de la bola, lo que causa turbulencia, que a su vez crea un centro de presión fuera del centro. La fuerza vertical ahora está arriba y es mucho más grande. Incluso más grande que el Efecto Magnus en flujo libre. Esto muestra que la bola se autocentraría y se autocorregiría. La fuerza axial es más o menos la misma que antes, como se esperaba.
Apartado 6: ¿Cómo encajan los cañones de largo alcance (LRB) en todo esto...?
El mod LRB en airsoft es donde el cañón se dobla hacia abajo para impartirle un giro a la bola haciéndola rozar la parte superior del cañón, en su camino de salida. ¿Cómo funciona si la bola se mantiene en el centro mediante un colchón de aire? En pocas palabras, la fuerza que lo empuja hacia la superficie superior, debe ser mayor que la fuerza que lo mantiene centrado. Hagamos las matemáticas para resolver qué está pasando y cómo funciona:
Pongamos un cañón de 30 cm y una potencia de salida de 350fps= 106.68m/s.
El SUVAT nos da una aceleración de 18967.7 metros por segundo al cuadrado, pero lo más importante, un recorrido de 0.0056s en el cañón. Supongamosme a la bola un peso de 0.2 g para ese disparo de 350 fps. Independientemente del peso, la fuerza aerodinámica autocentrante es de aproximadamente 0.15N. Estos resultados sería diferentes para diversas relaciones de medidas y peso de bola y diámetro de cañones y su magnitud está descentrada. Fuerza igual a masa por aceleración, significa que esto lleva a una aceleración de 750 m/s/s. Volviendo a los resultados del SUVAT, para encontrar que el desplazamiento vertical sería de 11.86 mm sobre ese cañón de 30 cm. Por lo tanto, si tu cañón de 30 cm de longitud se dobla en más de 11.86 mm y está disparando una bola de 0.2 g a 350 fps, entonces la bola se pondrá en contacto con el cañón. Esto podría sugerir una razón por la cual no son muy comunes también. Para un peso diferente de bola o diferente potencia de salida, necesitarías un cañón diferente. Por ejemplo, para 0.2 g de peso de bola, a 500 fps, 509 mm de cañón, y el desplazamiento sería de 16.73 mm.
Sería una configuración muy rígida. Las tolerancias de fabricación harían que cada arma disparara consistentemente a ellas, pero completamente diferentes unas de otras. Cada una podría tener una leve inclinación a la izquierda/derecha, que pueda ser difícil de corregir debido a la falta de ajuste en la configuración. Perfecto para modders técnicamente capaces tal vez, y demasiado restrictivo para los demás.
Imagino que tu consigues un efecto de hop mucho más consecuente de este método, porque no hay partes en movimiento. El hop up moderno se deformado ligeramente de manera diferente con cada bola que pasa por el, lo que dará lugar a alguna variación entre disparos. El acero no cede... vale... cuando lo comparas a las gomas de silicona...
Apartado 7: ¿Qué pasa con los cañones de ánima ancha? (6.23mm por ejemplo)
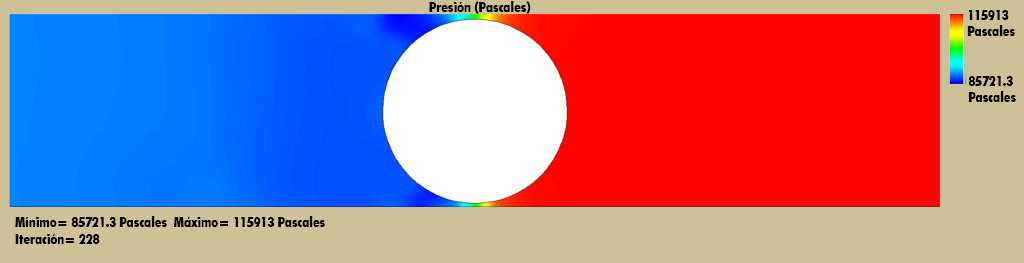

Centrado:
Fuerza (X) [N] 0.001410775192
Fuerza (Y) [N] -0.01125947496
Fuerza (Z) [N] 20.16382565
Descentrado, con la misma cantidad (0.025mm) que el cañón de modelo de 6.01:
Fuerza (X) [N] -0.004697257464
Fuerza (Y) [N] 0.06429097636
Fuerza (Z) [N] 20.158691
Lo que esto significa:
Lo primero a tener en cuenta, es que la fuerza del eje Z es menor que en el cañón de 6.01 en ambos casos. Tal como se esperaba, y encaja bien con los resultados experimentales de una caída de FPS que se sabe que produce un cañón de más diámetro. La magnitud de la caida en la fuerza es menor de lo que explica la magnitud de la caida de FPS. Pero esto es así debido a que estudiamos un modelo de estado estacionario. En realidad, la fuerza se vería reducida hasta casi cero, tal como la bola acelera en su transcurso por el cañón. Con un cañón de diámetro ancho, la presión cae más rápido que con uno estrecho, debido al incremento de un mayor volumen de aire. El soplado de aire en el cañón de 6.01mm fue 0.001219999 kg/s. Para el de 6.23 fue 0.005544020306 kg/s. Eso es 4.5 veces más aire pasando alrededor de la bola.
La fuerza del eje X no es realmente relevante para los propósitos de ésta investigación. Cabe señalar que es bastante pequeña.
La fuerza del eje Y es el foco de ésta investigación. Para un cañón de 6.01mm centrado, resultó en una fuerza inversa Magnus de -0.0077N. Para el modelo de 6.23mm centrado, la fuerza de Y es de -0.01126N. Esto representa un incremento de un ~30% en fuerza de Magnus inversa. Esto tiene sentido ya que tiene más aire moviéndose alrededor de la bola en dirección inversa.
El descentrado del modelo de 6.01mm dio 0.143N intentando volver al centro. Para el de 6.23mm dio un resultado de 0.0643N. Esto es una caida del ~45% en fuerza. Esto significa que la fuerza que intenta hacer volver la bola al centro, en un cañón de de diámetro ancho, es menor que en uno de diámetro corto, para la misma presión, y desplazamiento. Esto tiene sentido porque el efecto Bernoulli trabaja en diferencia de abertura relativa:
En un cañón de 6.01mm, la bola, cuando se centra, está 0.03mm de las paredes internas del cañón. Cuando la desplazas hacia abajo 0.025mm, está a 0.005mm de la superficie de abajo, y a 0.055mm de la parte superior. Eso es una relación de 11:1.
Para un cañón de 6.23mm, tiene un hueco de 0.14mm hacia el cañón cuando se centra. Cuando se produce ese desplazamiento de 0.025mm hacia abajo, está a 0.115mm de abajo y a 0.165mm de arriba, lo que le da una relación de 1.44:1, lo que es significativamente menos, con lo que el principio de Bernoulli y el Efecto Coanda se reducen proporcionalmente.
Para poner otro punto de perspectiva con esto: para el cañón de 6.01mm, la fuerza vertical se nos fue de -0.01126N abajo, a 0.0643N arriba. Eso es una oscilación de 0.07566N. En el modelo de 6.23mm varió de -0.0077N a 0.143N. Una fluctuación de 0.1507N. Eso es casi el doble.
Parecería que para la misma presión, la bola se mantiene más centrada en el cañón de 6.01mm que en el de 6.23mm. Para el mismo valor de FPS, se requeriría una presión mayor, lo que incrementaría la oscilación de la fuerza. Esto podría cambiar los resultados. Haría falta investigarlo más. Para llegar al fondo de esto, necesito saber lo que incrementa la presión para conseguir los mismos FPS en el cañón de 6.23 que lo que te dió en el de 6.01.
En este punto, los resultados no son concluyentes. Todo lo que se puede decir, es que siendo igual todo lo demás, un cañón de diámetro corto, debería de contener la bola centrada con más consistencia en su viaje a través del cañón, que uno de ánima más ancha.
Apartado 8: cañones de ánima ancha, investigación adicional




Para ser honestos, tú no usarías un arma lúdico deportiva con esa caida de FPS con un cañón a ánima ancha, y le pondrías uno de acorde a los límites que tuvieras. Un incremento de FPS se consigue con más presión de aire. O hasta cierto punto, un mayor volumen del mismo aire a presión.
No tengo datos para esto, así que haré una conjetura. Si tienes datos fidedignos, podrías mandármelos para volver a hacer estas pruebas.
Subo la presión un 15% y vuelvo a ejecutar. Los resultados son:
Fuerza (X) [N] -0.006858518
Fuerza (Y) [N] 0.013336395
Fuerza (Z) [N] 23.4898044
La presión está incrementando los FPS aproximadamente de manera proporcionada : de 20.158691N a 23.4898044N. No es importante el que esto no sea una relación directamente proporcional. Los cañones de ánima ancha experimentan más golpes, por lo que la presión cae más rápidamente mientras que la bola progresa por el cañón. Así que a pesar de que la fuerza inicial es más alta, caerá por debajo que en un cañón de ánima estrecha.
Lo más interesante es la componente vertical: fue de 0.06429097636N, pero la presión incrementada lo ha bajado a 0.013336395N. Esto es más probable porque el Efecto Magnus se incrementa más que el de Bernoulli, proporcionalmente a la diferencia de presión.
Por lo tanto, el subir la presión no mueve necesariamente la bola más centrada.
¿Qué pasa con el desplazamiento proporcional?
Vale, así que moviendo una bola 0.025mm hacia abajo en un cañón de 6.01mm de diámetro, hace una diferencia relativa mayor al hueco de aire que moviéndolo la misma distancia hacia abajo en un cañón de 6.23mm. El Efecto Bernoulli establece que las fuerzas no deberían ser equivalentes.
0.025mm hacia abajo en un caón de 6.01mm le da un hueco de aire en la parte superior de 0.055mm, y otro en la parte inferior de 0.005mm. Esto da una proporción de 11:1. Applicando esta misma proporcionalidad al cañón de 6.23mm hace que se desplace hacia abajo 0.116666666666667mm.
Remodelamos y volvemos a la presión estándar. Aquí están los resultados:
Fuerza(X) [N] 0.00075039
Fuerza (Y) [N] 0.346269096
Fuerza (Z) [N] 20.23075439
Ahora se da la cosa como realmente lo estaba esperando. La componente Z es practicamente la misma, X todavía es demasiado pequeña. Y se ha convertido en una magnitud importante.
Conclusiones
- Perderás FPS con un cañón de ánima o diámetro ancho.
- La bola se auto centrará en cañones de ánima ancha.
- Incrementar los FPS/presión es probablemente como mover la bola ligeramente abajo más que hacia arriba.
- A igual presión, y desplazamiento proporcional del eje del cañón, hacia la pared del cañón, los cañones de ánima ancha presentarán una mayor fuerza de auto centrado de la bola.
- Para el mismo desplazamiento desde el eje del cañón, los cañones de menor diámetro o ánima, tiene una mayor fuerza manteniéndolas en el centro.
- Las bolas en cañones de ánima estrecha, siguen un camino más estable que los de ánima ancha.
- La diferencia son micrones y probablemente irrelevantes.
Esto no es definitivo. Esto no quiere decir que los de ánima estrecha sean más precisos que los de ánima ancha. Puede ser que los cañones de diámetro mayor permitan una mayor amortiguación de las oscilaciones entre las interacciones con las paredes del cañón, lo que produce un vuelo más estable en el extremo del cañón. Puede ser que haya algo más que no haya descubierto o haya pensado en ello y es algo que produzca una mayor diferencia.
Apartado 9: Conclusión
Y todo esto suponiendo que se usa la misma presión. En realidad, la incrementarás para mantener los mismos FPS. Esto aumentaría las fuerzas de Bernoulli y Coanda que mantienen centrada la bola. Para obtener éste modelo, necesito saber qué presión necesita un cañón de 6.23mm para conseguir los mismos FPS que da uno de 6.01mm para una presión dada, preferiblemente la que he usado en este modelo.
Este modelo no tiene una entrada de volumen fijo como la tiene un arma lúdico deportiva de airsoft. Pero la bola también no presenta movimiento en el Eje Zmientras avanza por el interior del cañón, con lo que no cambia el momento de captura y cálculo de éste modelo. Esto es debido principalmente a las limitaciones del software, ya que no puede mover componentes de manera dinámica. Sin embargo, el modelo debería ser indicativo para los resultados en el mundo real.
Reconozco que todo esto es investigación puramente teórica, y no física, ya que no he realizado pruebas reales. A pesar de que esto deja lugar a las dudas, ya que "el mapa no es el territorio", es completamente plausible que la realidad del asunto sea completamente diferente. Todos los principios científicos, experimentos llevados a cabo, y modelos realizados por ordenador, sugieren que esto es así. Hasta que no pueda observarse en un experimento físico real, no se puede decir con certeza que este no sea el caso, y en este momento, todo lo que puede decirse es que esta es nuestra mejor comprensión.
En el futuro, me gustaría corroborar estos resultados con las pruebas que mencioné al principio de éste artículo, usando un cañón transparente y una cámara de alta velocidad. Entonces es cuando todo este asunto podrá ser finalmente aclarado. Supongo que otra alternativa sería hacer una foto del interior del cañón mientras la bola hace su avance por su interior, tal vez con una luz detrás para ver los huecos alrededor de la bola. He escuchado que esto se ha intentado varias veces, pero no he encontrado nada de fotos, videos o resultados online.
Estoy en esto por el conocimiento. Quiero que nosotros, como colectivo, entendamos el mundo mejor. Que nos permitan hacer mejoran que beneficien a todos. Estoy ciego a mis propios fallos. Es solo a traves de identificar estos fallos que podemos mejorar. Si tienes cualquier tipo de recomendación, mejora o información adicional, me gustaría escucharla. Como colectivo somos más fuertes y más capaces que cualquier individuo solo.
